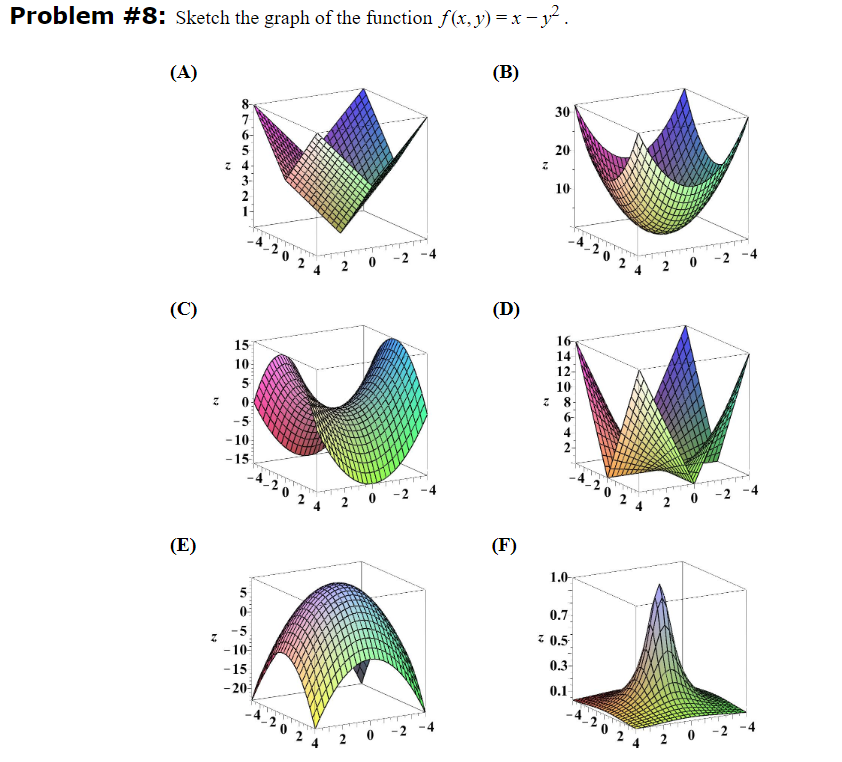
コンプリート！ x^2 xy y^2 グラフ 712596-X^2+xy+y^2 グラフ

 z＝x^2＋xy＋y^2って高校レベルでグラフかける？ 29コメント 3KB 全部 1100 最新50 ★スマホ版★ 掲示板に戻る ★ULA版★6．1 z＝xy のグラフ 原点（0,0,0)で、y＝x方向へは下に凸、y＝－x方向へは上に凸の曲面でる。このような形を" 馬の鞍型"という。 6．2 z＝（x＋y） 2 のグラフ 長方形の紙の両辺を持ってゆっくり曲げた感じの曲面。y＝x方向に、放物線 y＝4x 2 が連なっている。 6．3 z＝x 2 ＋y 2 のグラフ 円周を不等式 y>x 2 の表す領域は方程式 y=x 2 の表す曲線の上側 不等式 x>y 2 の表す領域は方程式 x=y 2 の表す曲線の右側 (3) 円のように縦線で切っても横線で切っても境界線が2つできるような図形は、境界線よりも上（下）という示し方でも境界線よりも右（左）という示し方でも示すことができない。

陰関数とは 意味や陽関数との違い 微分のやり方 グラフ 受験辞典

X^2+xy+y^2 グラフ

X^2+xy+y^2 グラフ-条件式付きの2変数関数の最大・最小 条件式が一次 条件式が一次（範囲あり） 条件式が二次 条件式なしの2変数関数の最大・最小 まとめ！ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる！ こちらの関連記事はいかがでしょうか？青のグラフ： 曲線 x 3 y 3 3xy = 0． 赤のグラフ： 曲線 F y (x, y) = 0， すなわち y 2 x = 0． 赤の曲線と交わっていない点 (a, b) (a ≠ b 2) の近くで，青のグラフは y = f (x) の形式になっていることがわかる 画像19． 青のグラフ： 曲線 2x 2 xy y 2 2x 3y10 = 0．

What Does X Y 2 Look Like On A Graph Study Com

積分電卓 積分する関数を入力してください 変数 被積分関数 x/ (x^2y^2) を次の変数で微分する x log (y^2x^2)/2 注意 log 自然対数 グラフを描く LaTeXエディタで編集 このページへの直接のリンク 積分電卓 解析積分を用いて所与の変数に対する関数の不定2 z = √ x x2y2 のグラフ よって， lim (x;y)→(0;0)x √ x2 y2 は存在しない． O y r x r (注意) lim(x;y)→(0;0)f(x, y) を調べるのに有効な方法として，x = rcosθ, y = rsinθ（極座標変換）とおき，(x, y) → (0, 0) の代 わりにr → 0 とする方法である．これは，点(x, y) が原点 に近づくことは距離が0に近づくこととっていう名前がついてるよね？？ でもときどき、 どっちがx軸で、どっちがy軸なのか？？ってことを忘れちゃうわない？？ 座標軸の「x軸」と「y軸」の覚え方を

Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge問題18 z = f(x;y) = x2 xy 2y2 x 2y で定義される関数のグラフを描きたい (1) うまいa, b を見つけてX = x a, Y = y b と置くとf(x;y) はf(x;y) = AX2 2BXY CY2 という形にできる このようなa, b, A, B, C を求めよ (2) z = f(x;y)のグラフの概形を描け 略解 (1) a = 2 3, b = 1 3, A = 1, B = 1, C = 2 (2) 略 問題19 f(x;y) = 8 < x y3 x2Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge

一般に，f(x,y)のグラフz = f(x,y) z = xy, (x,y,z) = (−2,3, −6) f を(4)と同じ関数として，接点(2,3,6)における接平面の法線ベクトルは (fx(−2,3),fy(−2,3),−1) = (3,−2,−1) で与えられる。接平面の方程式は 3(x2)−2(y −3)−(z 6) = 0 (6) x2 y2 z2 = 1, (x,y,z) = (0,0,1) この曲面は原点を中心とする半2 のグラフはy= x2 のグ ラフにy= x 2 1 2 のグラフの高さを足したものですが、全体として下に凸の放物線であることに 変わりありませんでした（図6）。このことは、 x2 x 2 1 2 = (x 1 4)2 7 16 と平方完成してみればはっきりします。これと同じようなことが22} のグラフ {(x,y) ∈ R2;

70以上 Y X 2 2 Graph Y X 2 2 9 Graph Josspix0eyb

基本 無理関数のグラフ 放物線の一部 なかけんの数学ノート

 問題文に「実数」という単語があり，2文字の対称式が条件として与えられた2変数関数の最大最小問題の考え方と解法を説明します。 問題文に「 x, y は実数とする」なんてあっても気にしない人が多いのではないでしょうか。 また，与えられている条件式Plotfoox, {x, 1, 1}, PlotLabel > "y=x^3 x^2 x 1" とやれば，グラフの名前として「y=x^3 x^2 x 1」を表示してくれる． Plotfoox, {x, 1, 1}, PlotLabel > "y=x^3 x^2 x 1", PlotRange > {4, 4} とすれば，y軸を4から4までの範囲でグラフを描いてくれる． Plotfoox, {x, 1, 1}, AxesLabel > {"x", "y"} とかやれば，x軸とy最後に、上のyxグラフから、波の式を立ててみよう！ 波は、さっきの問題とは逆方向に、速さ\(v\)で進むよ！ 塾長 ※いつも通り、まずは自分で考えてみましょう！自分で解くことで、『解くうえで何が足りないのか』が明確になります！ まずは、（\(yx\)）グラフを（\(yt\)）グラフに書き換え

1

12年京大入試理系数学第3問その1 ほのぼの数学がんばろう

Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge右図3のように，1つの x に対応する y が2つあるグラフの方程式は， y=f(x) の =r より x 2 y 2 =r 2 ※ 点 P が座標軸上（通俗的に言えば，赤道上または北極，南極の場所）にあるとき，直角三角形にならないが，たとえば x 軸上の点 (r , 0) についても， r 2 0 2 =r 2 が成り立つ．このように，座標軸F(x,y) グラフ(つまり(x,y,f(x,y)) の定める曲面)となる。 練習問題 z = x2 y2、z = x2 −y2、z = xy が定める曲面の 概形を求めよ。 ヒント を固定したときに 一定の平 面上に 、 、 が定める曲線を考 える。 微分積分・同演習B – p6/18

Y Sin 2x のグラフや周期は Y Sin 2 8を微分するとどうなるのか ウルトラフリーダム

Surfaces Part 2

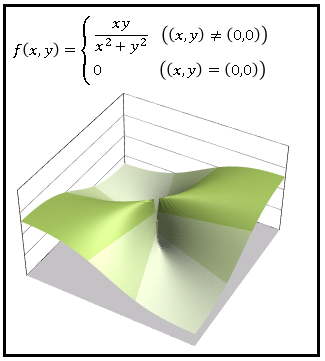
Xy x 2y (x,y) 6= (0,0) 0 (x,y) = (0,0) のとき． 1 f(x,y) は(x,y) = (0,0) においてx,y に関して偏微分可能であるが，連続ですらな い（従って，全微分可能ではない）．実際 lim x→0 f(x,0)−f(0,0) x−0 = 0 より，f x(0,0) = 0．同様にf y(0,0) = 0．しかしlim x→0 f(x,x) = 1 2 6= 0 より，f(x,y) は(0,0) で連続ではない． 定理55グラフ x^2y^2=4 x2 y2 = 4 x 2 y 2 = 4 これは円の形です。 この形を使い円の中心と半径を決定します。 (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 この円での値と標準形での値を対応させます。 この変数 r r は、円形の半径を表し、 h h は、原点からx軸方向の右図のような2次関数になり， x=1 （このとき y=1 ）のとき最大値 1 になる． 例題12 x2y=3 のとき， 2x 2 y 2 の最小値を求めてください． 条件式の方程式を使って1文字を消去しますが， y を消去すると初めから分数が登場します． この形なら x を消去

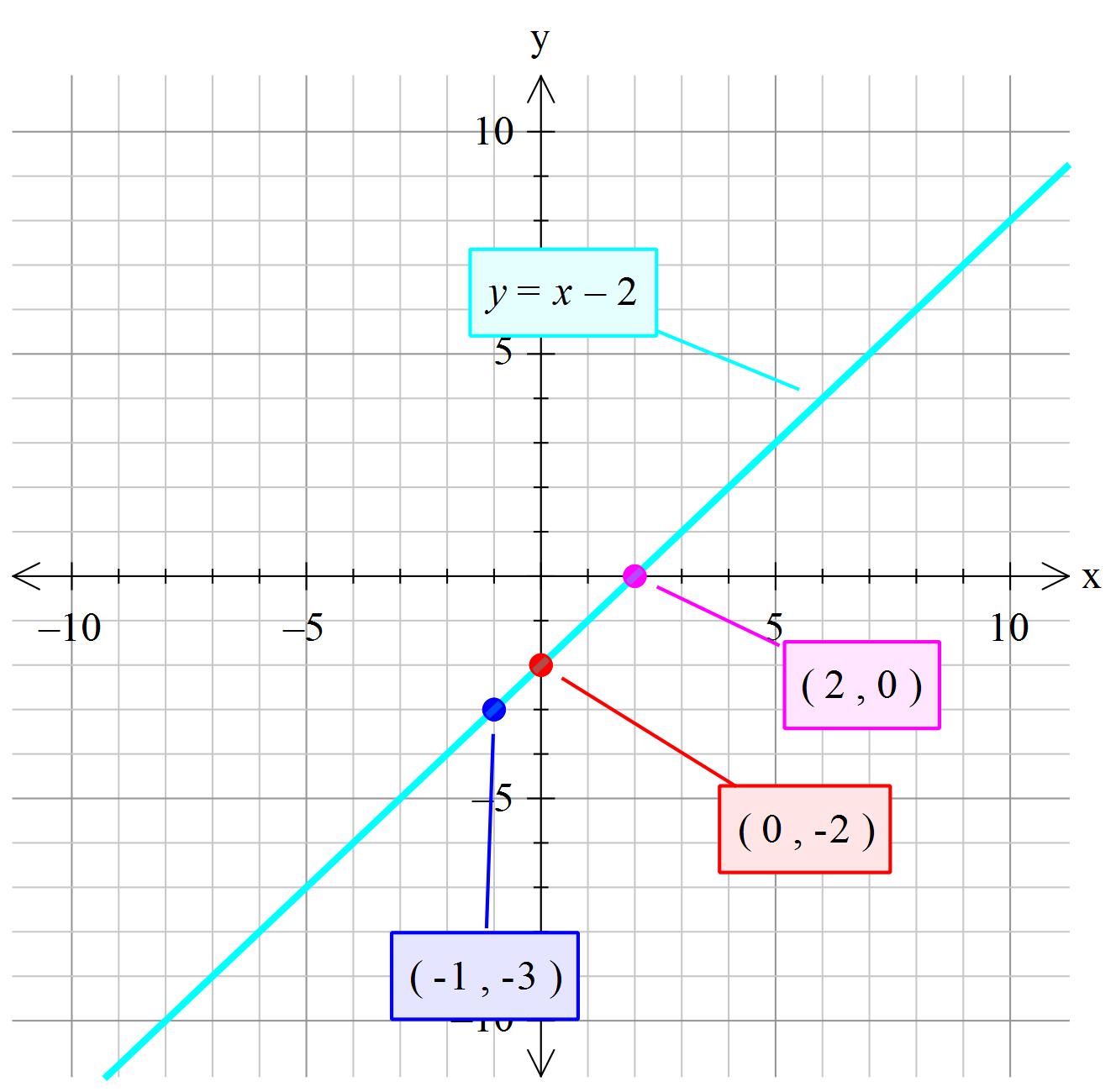
How Do You Graph The Line X Y 2 Socratic

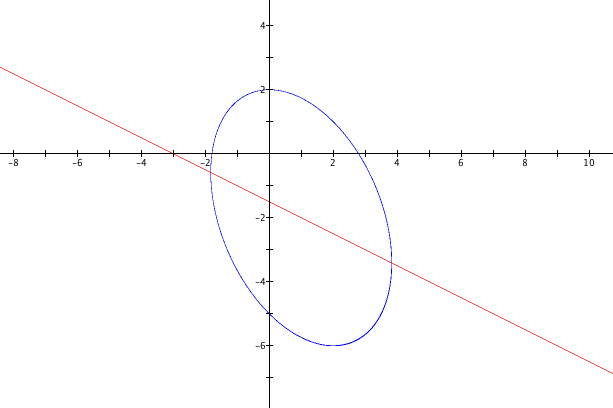
微積のページ

§ 簡単な無理関数のグラフ xy座標平面において，区間0,∞) を x y 0 1 1 y=x2 ( x≥ 0 ) y= √ x y=x 定義域とする関数 y= √ x のグラフ を描きます．関数g が関数f の逆関 数であるとき，y=g(x) のグラフは y=f(x) のグラフと直線 y=x に関 して対称です（定理77）．81節The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}2yxy^ {2}=0 x 2 2 y x y 2 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2y for b, and y^ {2} for c in the quadratic formula, \frac {b±\sqrt {b^ {23x^22xyy^2=1のグラフ WolframAlpha 円の面積が簡単に求められます． Proのご購入 NEW 教科書の数学表記で入力できます．

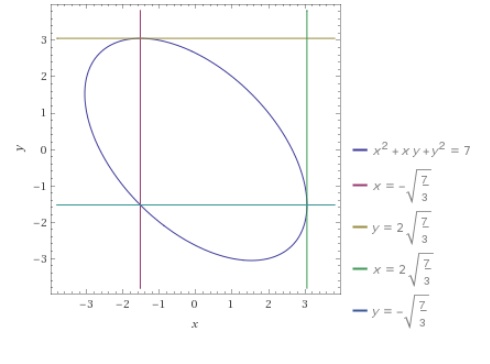
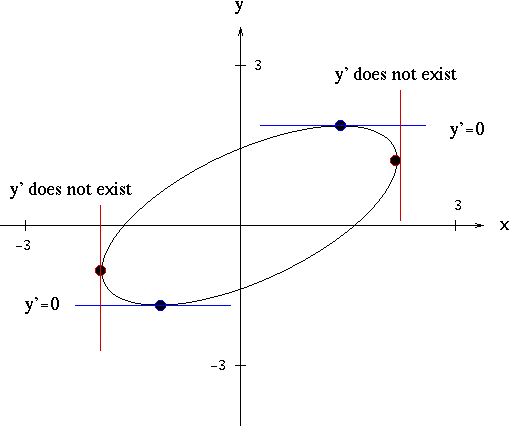
How Do You Find All Points On The Curve X 2 Xy Y 2 7 Where The Tangent Line Is Parallel To The X Axis And The Point Where The Tangent Line

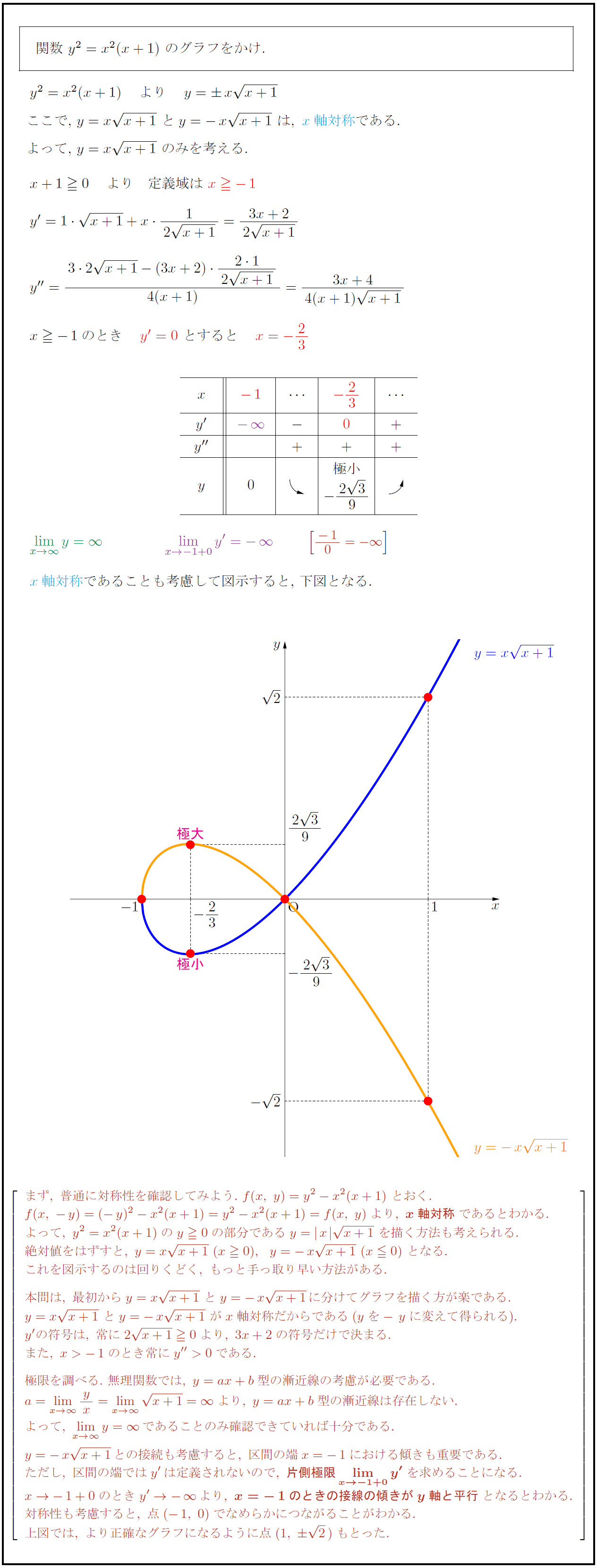
高校数学 陰関数 Y X X 1 のグラフ 受験の月

 散布図（XYグラフ）を作成する グラフ化するデータ範囲を選択します。 （下図の例では、C2D12を選択しています。 ) 挿入タブの 散布図 (X,Y)または バブルチャートの挿入→ 散布図を実行します。 散布図が作成されました。Y=(x−2)−3=x−5 y=−(x−2)−3=−x−1 問題 (1) 中学校で習う直角双曲線xy＝aは、一般的双曲線x2／a2－y2／b2=1の特殊解として導くことはできるのでしょうか？教えて下さい。 ＝＞作者：連絡ありがとう． (A)の に特定の値を与えると， (B)の形になるかという問いでしたら，そうではないZ = f(x,0)} を描け． (1) f(x,y) = x2 − y2 (2) f(x,y) = √ x2 y2 (3) f(x,y) = 1 x2 y2 Ex22 次の直線に沿って(x,y) が(0,0 に近づくとき，関数f(x,y) = x − y x y の極限値を求 めよ． (1) 直線y = x (2) x 軸． (3) y 軸． Ex23 以下の2

図形のファイル

大川研究室数学の問題コーナーに挑戦

Y=ax 2 のグラフを，x 軸方向へ p，y 軸方向へ q だけ平行移動する。そこで，X=xp，Y=yq とおくと，x=Xp，y=Yq となるので，与式へ代入すると，Yq=a(Xp) 2 よって， ﾜﾝﾎﾟｲﾝﾄ ① この式も右式を展開すると，2 次関数の一般の形になります。つま り展開しますと， y=ax 22apxap 2 q となり，b=2ap,c美しいグラフを自由自在に描ける無料のオンライングラフ計算機。関数のグラフや点をプロットできるのは勿論、方程式の解を求めたり、スライダーを使ってグラフを動かしたりできます。 無題のグラフ ログインまたはサインアップ 1 2 提供： 提供： "x" $$ x "y" $$ y "a" squared $$ a 2 "a¶ 基礎数学II：2変数関数は3D グラフ ‡ 関数 f(x,y) = 2x2 2xy y2 −6x−4y 代入 f(3,2) = 2·32 2·3·222 −6·3−4·2 = 8 グラフ z = f(x,y)6 ¡ ¡ ¡ ¡" ¡ ¡ r r r d d¡" 6 HHj HH 8 3 2 z x y µ 問1 (x−y 平面) 下のそれぞれのグラフに、次の座標で示される点を打ちなさい。 ⃝1 (0,0) ⃝2 (1,0)

1

2変数関数と偏微分 グラフ 接平面を描いてみよう 趣味の大学数学

グラフを描画するには、カンマで区切って関数を特定し、グラフ領域XとYの範囲を指定して、"グラフを描く"ボタンをクリック。 数式の書式を表示 例 1/x, x sin(x), 11, 11 (trig, sin(x), cos(x)), (linear, x, 2*x1) (quadrants, green, 11, 11, 11, 11) (Ellipse, green, sqrt(1x*x/4), sqrt(1x*x/4)) (Piecewise, 2x*def(x, 0, 1F(x,y) = 1 2} を描け．また，y = 0 におけるグラフ{(x,z) ∈ R2;直角双曲線の平行移動 ･･･(2) 関数 y= のグラフを x 軸の正の向きに p ， y 軸の正の向きに q だけ平行移動してできるグラフの方程式は y= q になる． 図1 (1)の詳しい解説→ (2)の例： y= 4 のグラフは， y= のグラフを x 軸の正の向きに 2 ， y 軸の正の向きに 4 だけ平行移動したものだ

二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局

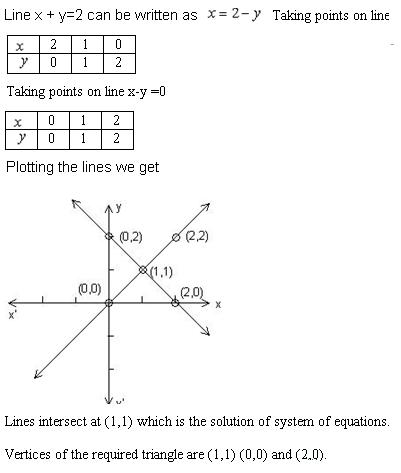
Draw The Graph Of X Y 2 And X Y 0 And Hence Find The Vertices Of The Triangle Formed By The Lines And The X Axis Mathematics Topperlearning Com Sljoqnfee

数学知識構造の全体を見るにはこのグラフ 応用分野： 因数分解の基本公式， 因数分解の公式 (xy)(x^2xyy^2) x 3 y 3 を x の関数と考えて f (x) = x 3 y 3 とおく． f (− y) = (− y) 3 y 3 = − y 3 y 3 = 0 よって，因数定理より f (x) は x − (− y) すなわち x y を因数に持つ． x 2 − x y y 2 _________ x定義：2次同次関数 、2次形式 ・「2変数x,yについての二次形式」「x,yの2次同次関数」とは、 2変数x,yについての多項式で、2次の項ばかりからなるもの すなわち、 Q (x,y) = ax 2 2 bxy c y 2 (a,b,cは定数) のことをいう。 ※詳細→2変数2次形式 文献(xy)2 (x y)2) と式変形してX = x y, Y = x y と置けば、bの正負に従ってz = X2 Y2 の場合か z= X2 Y2 の場合になります。よって、グラフの大体の形を調べるだけならa̸= 0 の場合の 議論だけですべての場合が尽くされていることになります。

大学数学 ２変数の関数と極限の考え方

Solution Consider The Graph Of X 2 Xy Y 2 1 Find All Points Where The Tangent Line Is Parallel To The Line Y X

< 2変数関数のグラフ> 2変数関数z = f(x;y) のグラフは曲面を表す。 とくにf(x;y) がx とy の一次式の場合は 平面を表す。 例1 f(x;y)=09x03y 05 の場合、z = f(x;y) のグラフは図1のように x軸方向の傾きが09 y 軸方向の傾きが03 z 切片が05 の平面を表す。 問1 f(x;y) が以下の場合に、z = f(x;y) の

陰関数とは 意味や陽関数との違い 微分のやり方 グラフ 受験辞典

What Are The Extrema And Saddle Points Of F X Y X 2 Xy Y 2 Y Socratic

基本 指数関数のグラフ なかけんの数学ノート

A The Graph Of F X Y X 2 Y 2 The Point 0 0 Is A Download Scientific Diagram

2x 2 2xy Y 2 4で囲まれた部分の面積を求める問題です Y に直し Clearnote

H 2 Ksuzuki Teaching 05 Ch2 Pdf آ 2 2 Z E X 2 Xy Y 2 W Sأ 2 1 5 1 0 5 0 0 5 1 1 5 2 2 1 5 1 0 5 Pdf Document

二変数関数の極限と連続 編導関数 Excel Vba 数学教室

Solutions To Implicit Differentiation Problems

大学数学 ２変数関数の極大 極小

微積のページ

X Y 2 グラフ

２０１３年 数楽工作倶楽部 ５

Solution Please Help Me With Those Problems Thanks 1 Graph X2 2xy Y2 1 2 If The Parabola De Fined By Y Ax 2 6 Is Tangent To The Line

図形のファイル

Solved 3 Consider The Graph Of X2 Xy Y2 1 0 5 0 5 A Chegg Com

2d 陰関数グラフ

Emat 6680

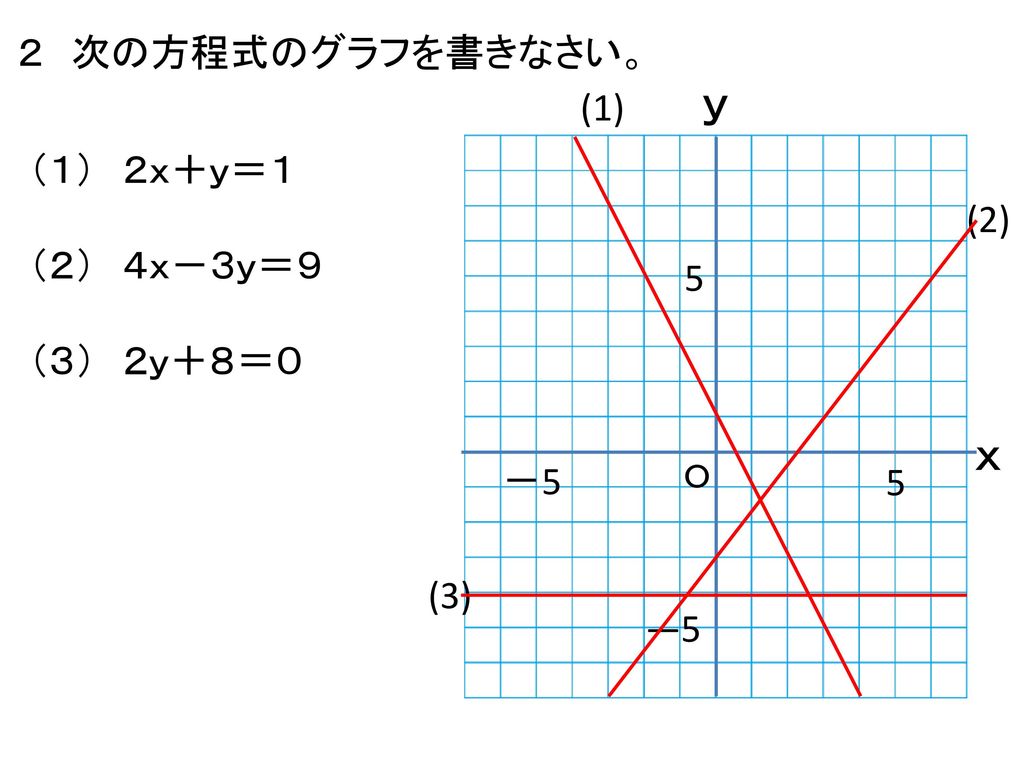
一次関数と方程式 本時の流れ ねらい 二元一次方程式をグラフに表すことができる 課題の提示 Yについて解き グラフをかく Ppt Download

２次関数のグラフ

基礎数学 6回目

実数x Yが X 2xy 2y 8 を満たすと Okwave

Graphs And Level Curves

F X Y X 2 Y 2のグラフの概形を見ましたがどうしてあの Yahoo 知恵袋

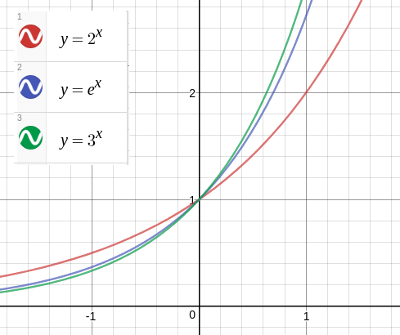
指数関数 初等数学 基礎からの数学入門

Draw The Graph Of The Equation Given Below X Y 2

Gcalc Plus

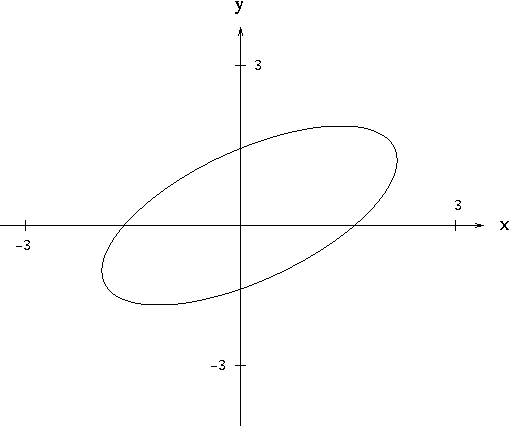
Implicit Differentiation

Solved The Graph Of Equation X 2 Xy Y 2 9 Is A Slanted Chegg Com

陰関数とは 意味や陽関数との違い 微分のやり方 グラフ 受験辞典

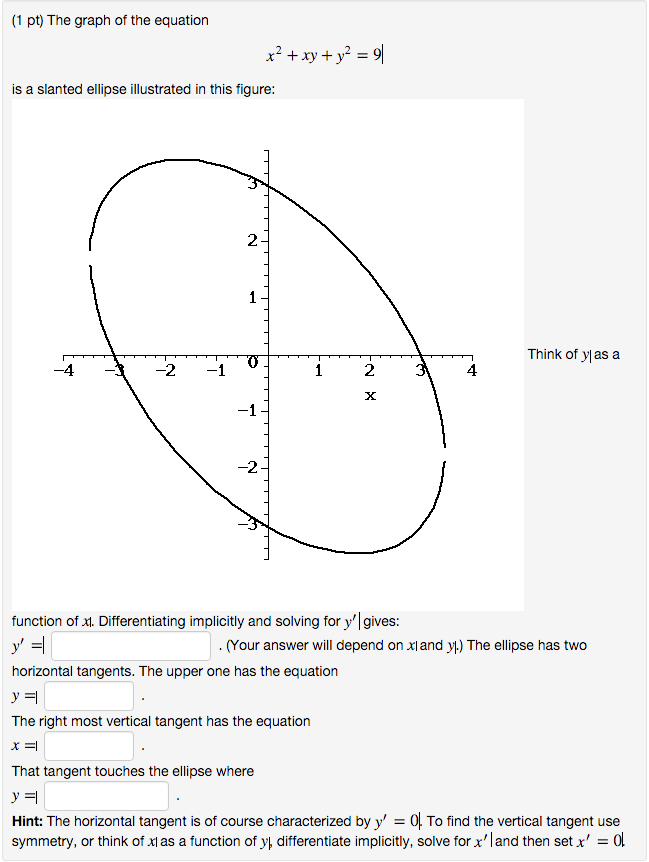
Solved The Graph Of The Equation X 2 Xy Y 2 9 Is A Chegg Com

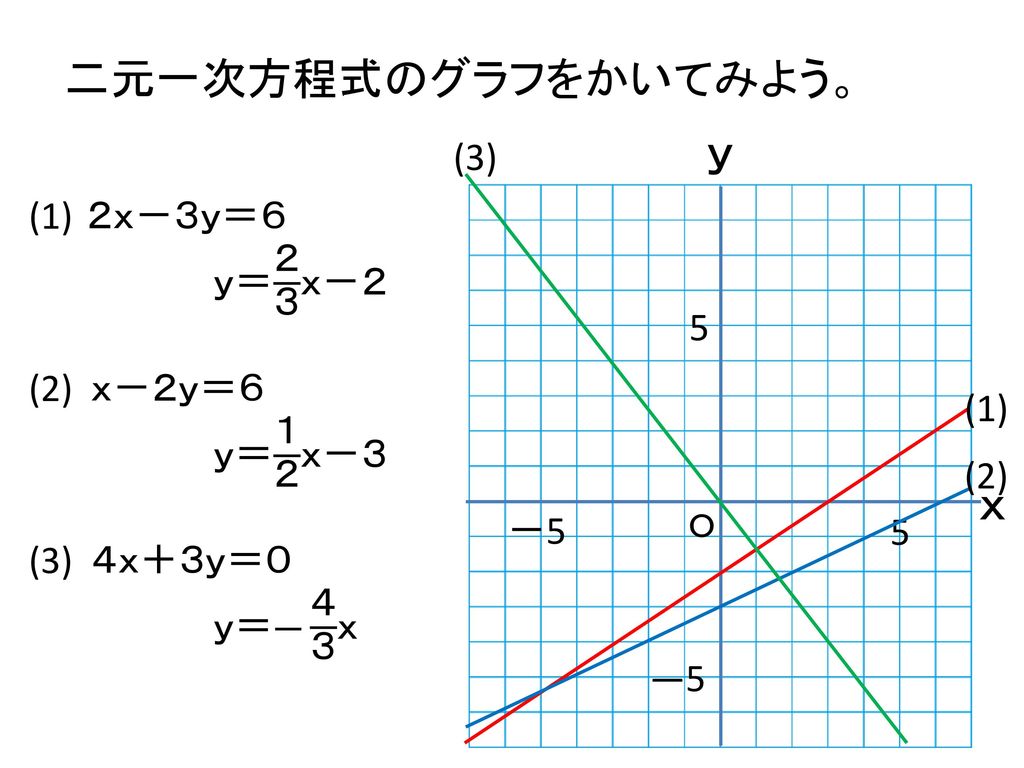
一次関数と方程式 本時の流れ ねらい 二元一次方程式をグラフに表すことができる 課題の提示 Yについて解き グラフをかく Ppt Download

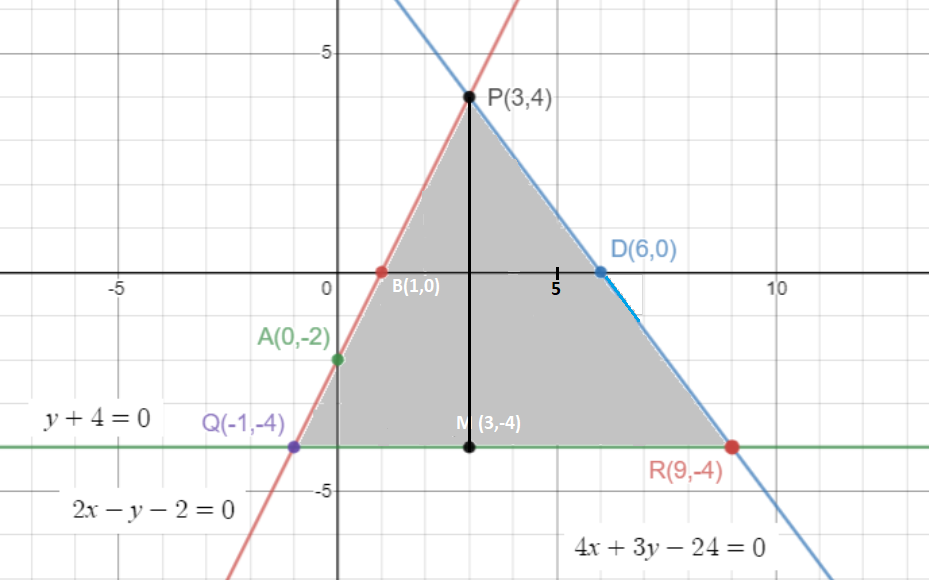
最も選択された 2x Y 2 Graph The Equation Graph The Equation Y X 2 2x 8 Hanpituhoang

Y 1 Xの属性 数学についてのwebノート

Scarpelli Assignment 2

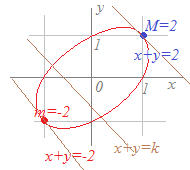
２次関数の最大値 最小値

Graphs And Level Curves

中１ 比例のグラフ

偏微分の意味とやり方

偏微分の意味とやり方

File Conic X 2 2xy Y 2 8x 0 Svg Wikimedia Commons

Graph Of A Function In 3d

X 2 Y 2 0のグラフってどうなりますか X Y X Y Yahoo 知恵袋

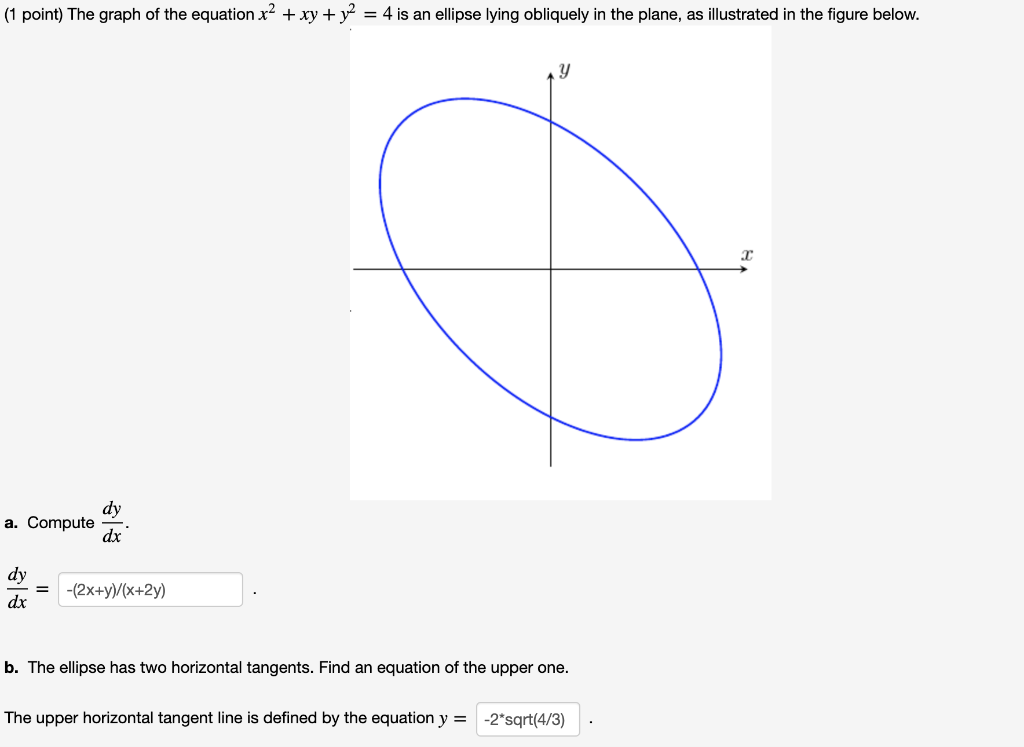
Solved The Graph Of The Equation X2 Xy Y2 4 Is An Ellipse Chegg Com

3 This 2d Example Where X Y Are The Configuration Parameters Download Scientific Diagram

2次曲線のグラフ 微積の授業中に2x 2 4xy 5y 2 6のグラフを書けという 数学 教えて Goo

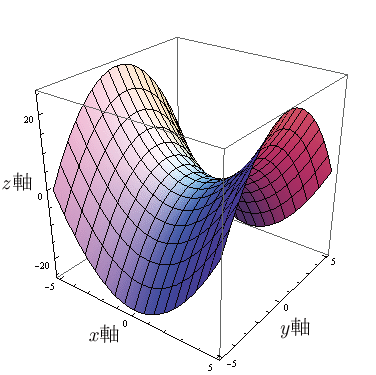
2変数関数

基本 二次関数y A X P 2のグラフ なかけんの数学ノート

Biational Map Between X 4 2x 3y 2x 2y 2 2xy 3 Y 4 Z 4 And Y 2 X 3 8x

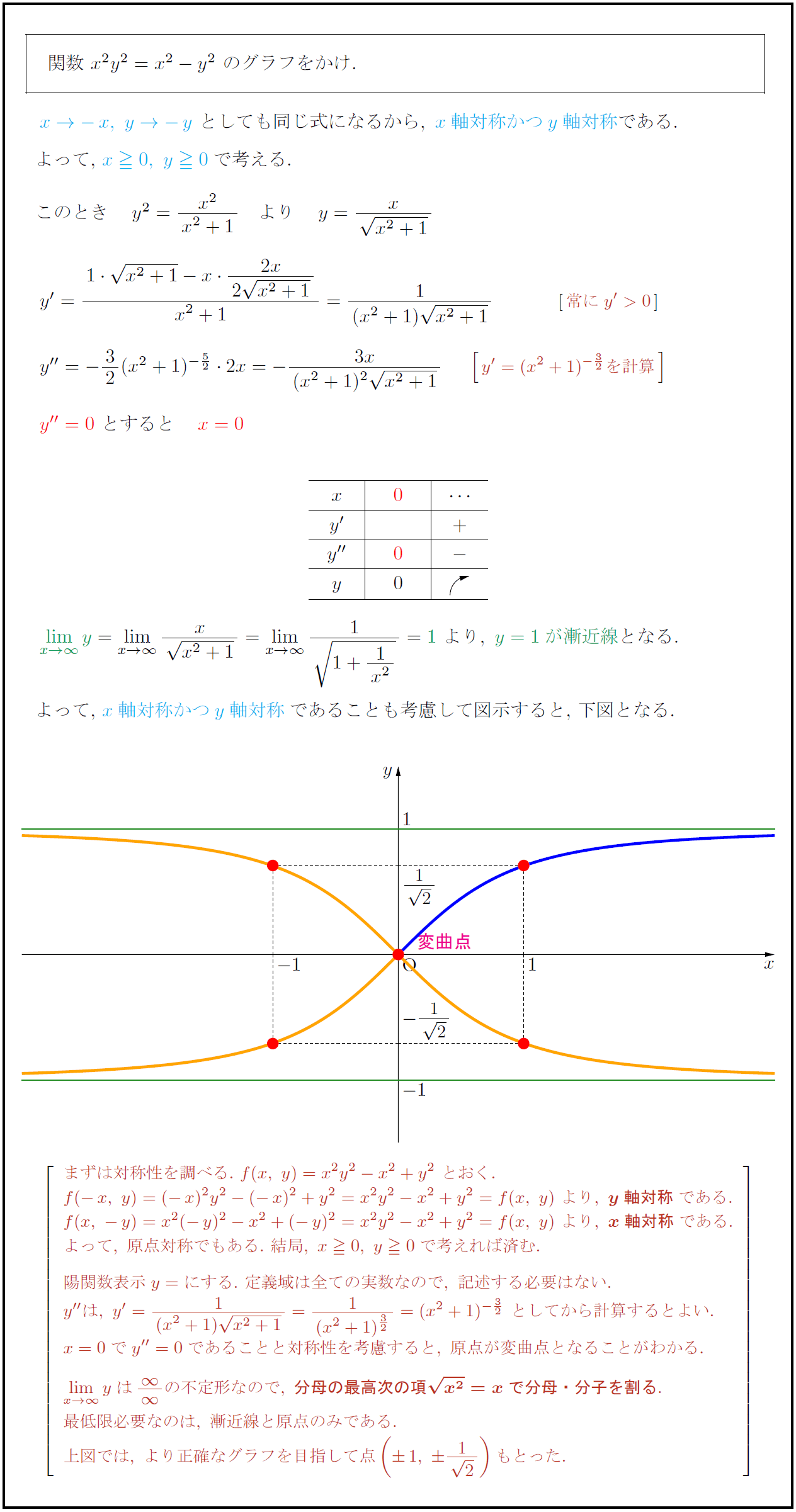
高校数学 陰関数 X Y X Y のグラフ 受験の月

図形のファイル

2次曲線のグラフ 微積の授業中に2x 2 4xy 5y 2 6のグラフを書けという 数学 教えて Goo

解説見てもよくわかりません Clearnote

Graph Of 2 Variable Functions

If F X Y 9 X 2 Y 2 If X 2 Y 2 Leq9 And F X Y 0 If X 2 Y 2 9 Study What Happens At 3 0 Mathematics Stack Exchange

21 Graph Of The Function F X Y 2xy C X 2 Y 2 C Used For L And Download Scientific Diagram

Graph The Region Bounded Between X Y 2 4y And X 2y Y 2 And Find The Area Study Com

What Does X Y 2 Look Like On A Graph Study Com

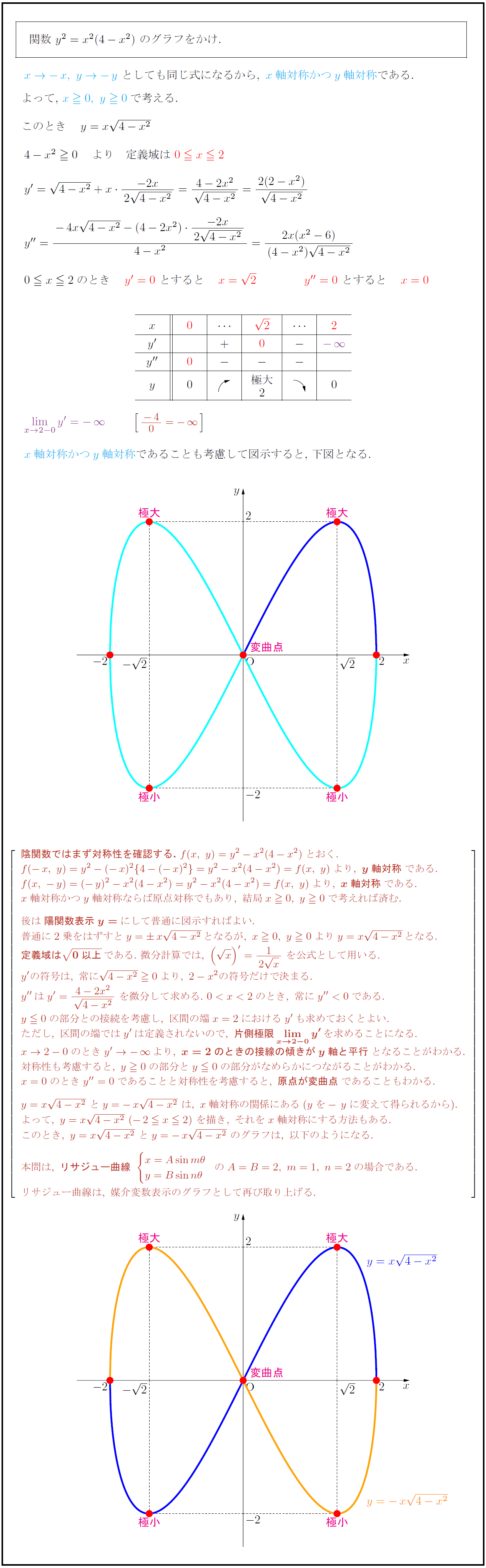
高校数学 陰関数 Y X 4 X のグラフ リサジュー曲線 受験の月

ｘ２乗 Y２乗 1を満たす実数x Yに対して 最大値と最小値を求めよ という Clearnote

０７年８月号の補足

2変数関数と偏微分 グラフ 接平面を描いてみよう 趣味の大学数学

File 3d Graph X2 Xy Y2 Png Wikimedia Commons

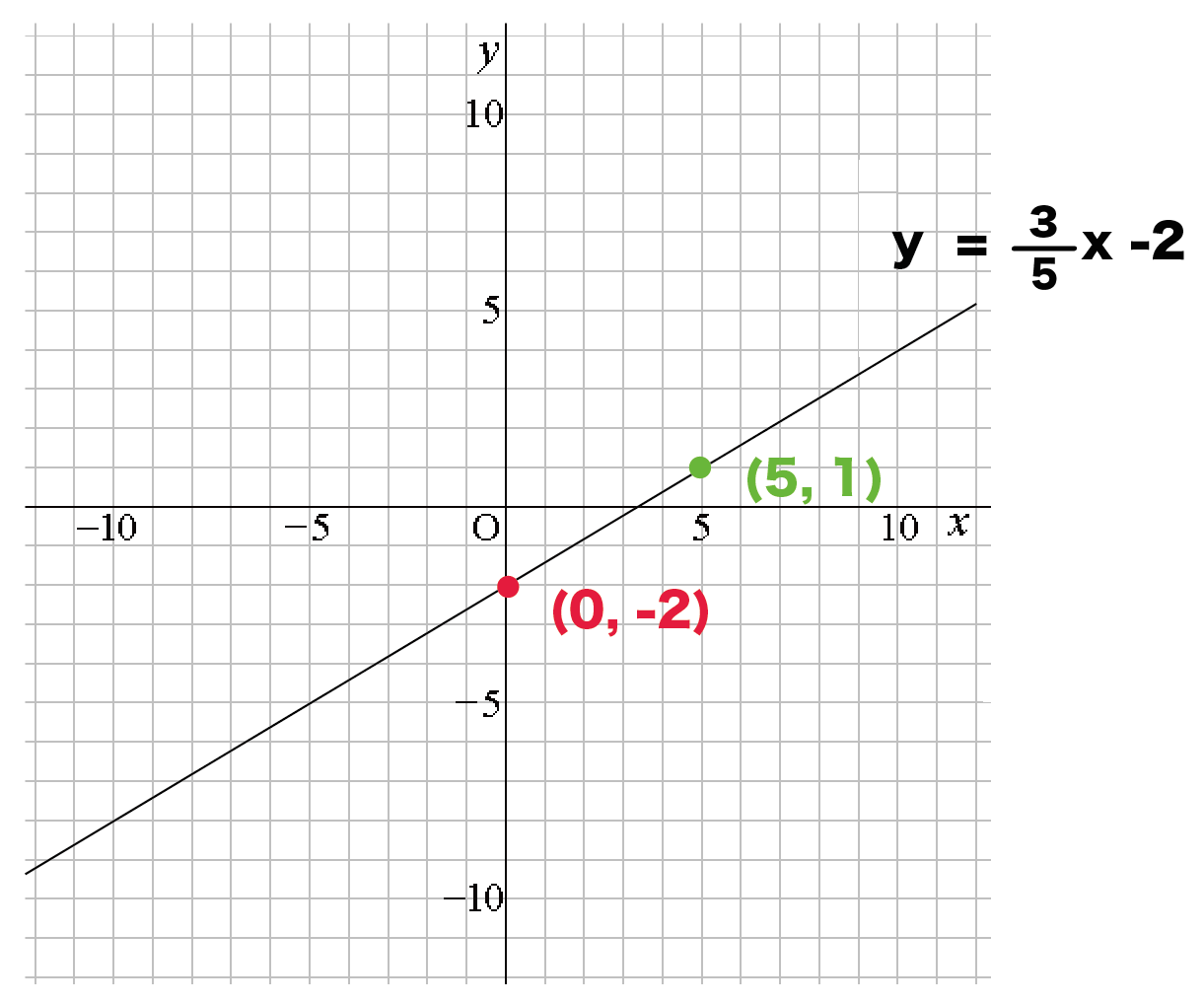
中2数学 一次関数のグラフの書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

基礎数学 6回目

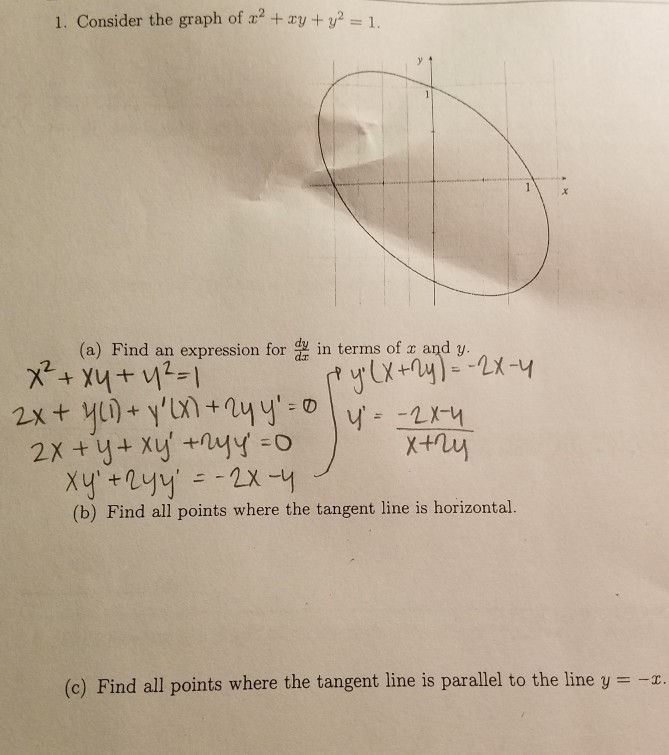
Solved Consider The Graph Of X 2 Xy Y 2 1 A Find An Chegg Com

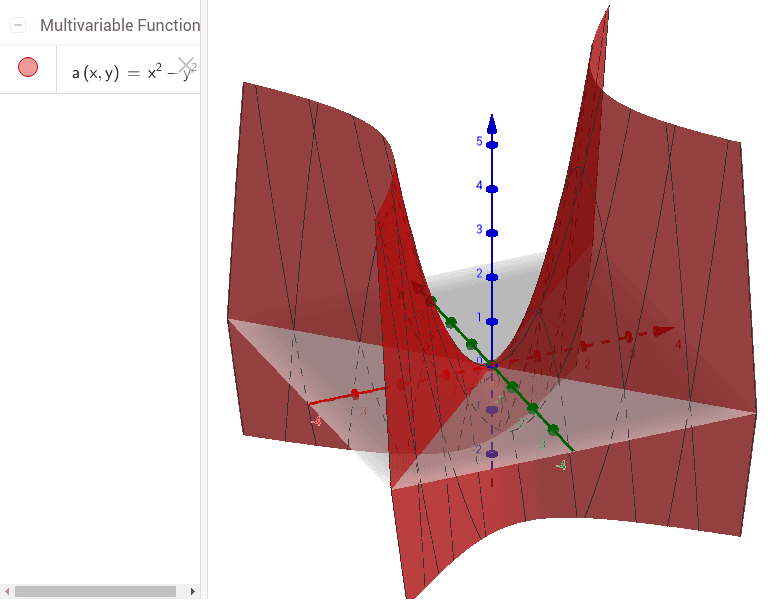
Graph Of F X 2 Y 2 Geogebra

図形のファイル

基礎数学 6回目

最適化数学のための Matx プログラミング

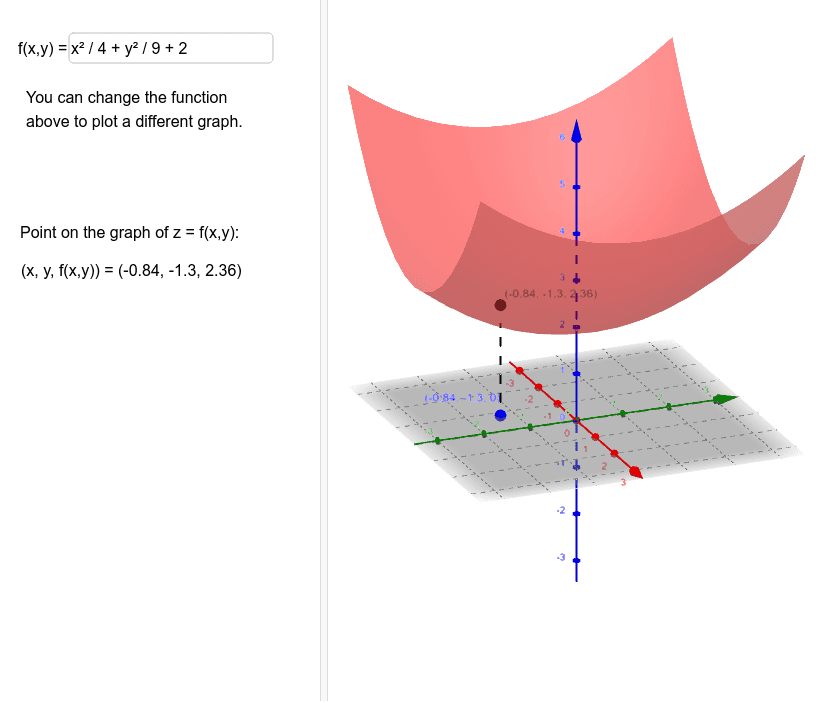
Graph Of Z F X Y Geogebra

X Y 2 And X 4 Y 2 Math Central

因数分解とグラフ 中学から数学だいすき

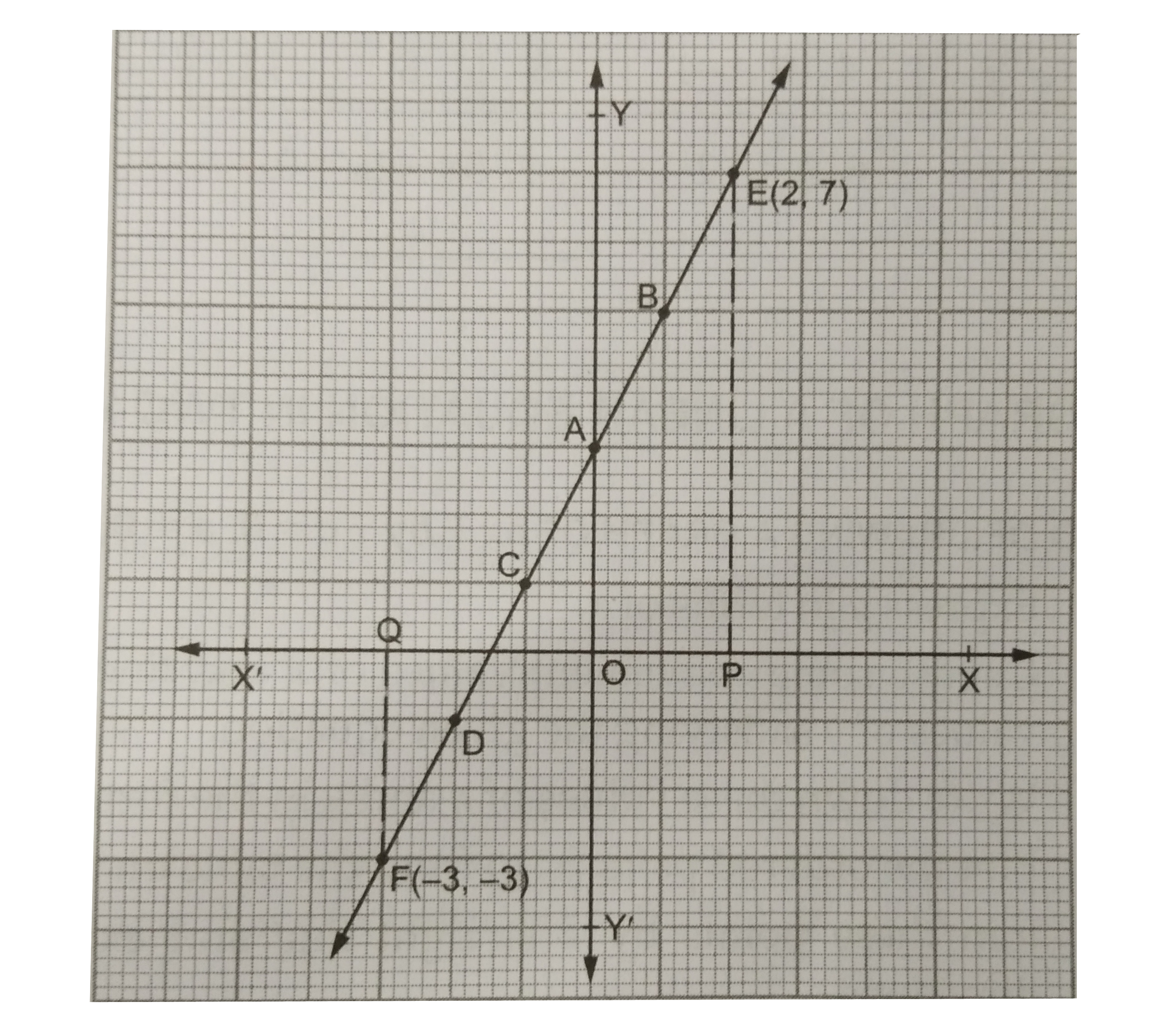
Draw The Graph Of The Equation 2x Y 3 0 Using The Graph Find The Value Of Y When A X 2 B X 3

重ね合わせの原理でグラフを描く

Gnuplot Demo Script Singulr Dem

File X Y 2 Svg Wikimedia Commons

How To Plot 3d Graph For X 2 Y 2 1 Mathematica Stack Exchange

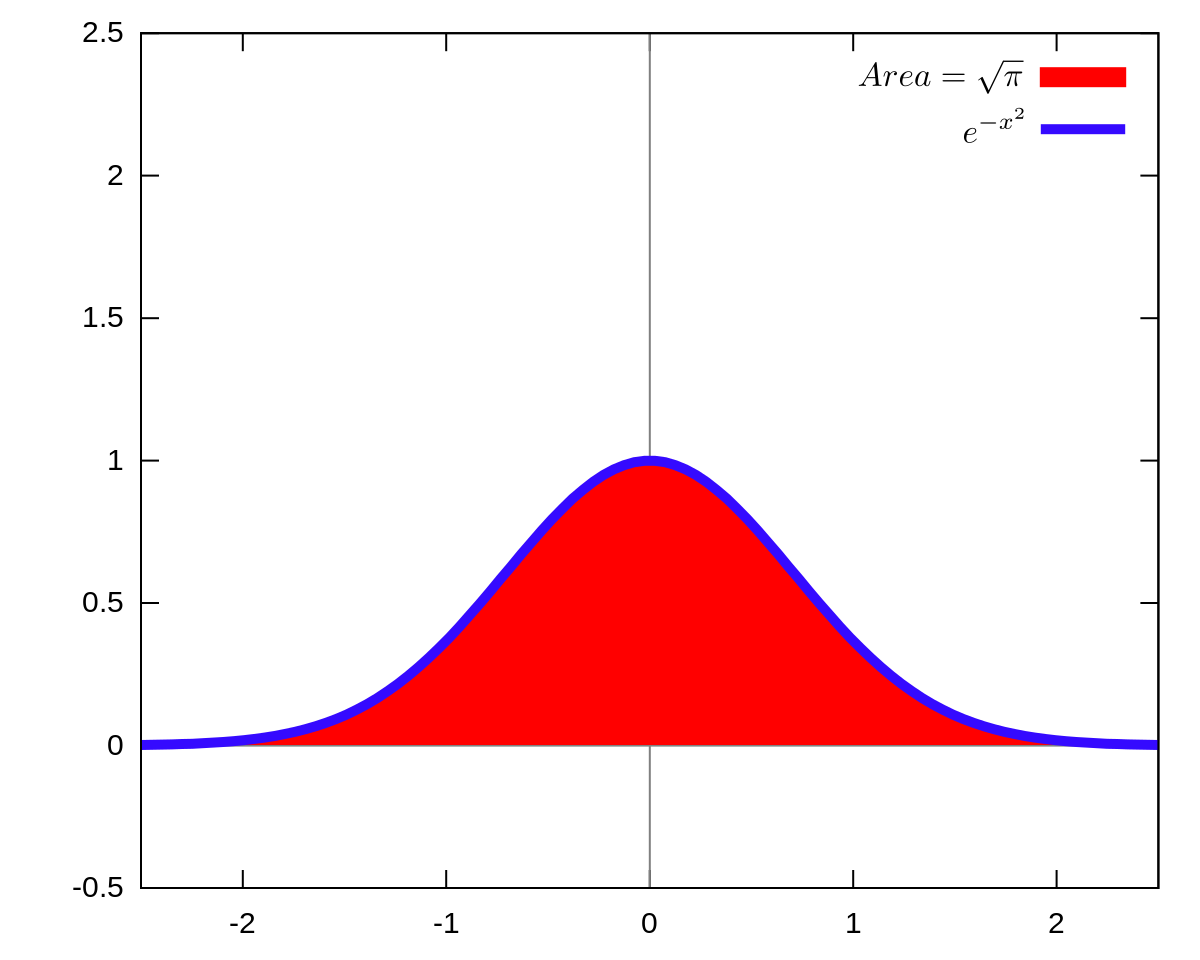
ガウス積分 Wikipedia

Draw The Graph Of X Y 2 Please I Need Answer Brainly In

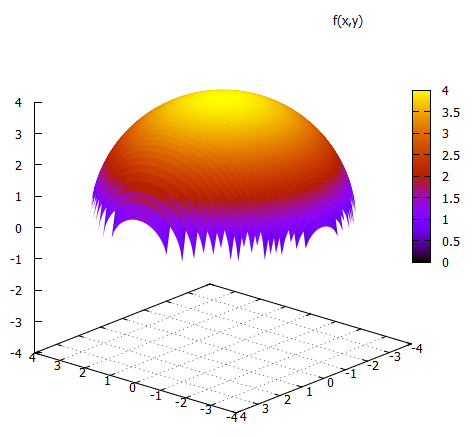
数学 2変数関数のグラフ 毎日学生気分

3年 関数 Y X のグラフ 数学イメージ動画集 大日本図書

If X 2 Xy Y 2 27 7 The Maximum 3x 2y Quora

X Y 2 And X 4 Y 2 Math Central

1

Ex 6 2 5 Solve X Y 2 Graphically Chapter 6 Cbse

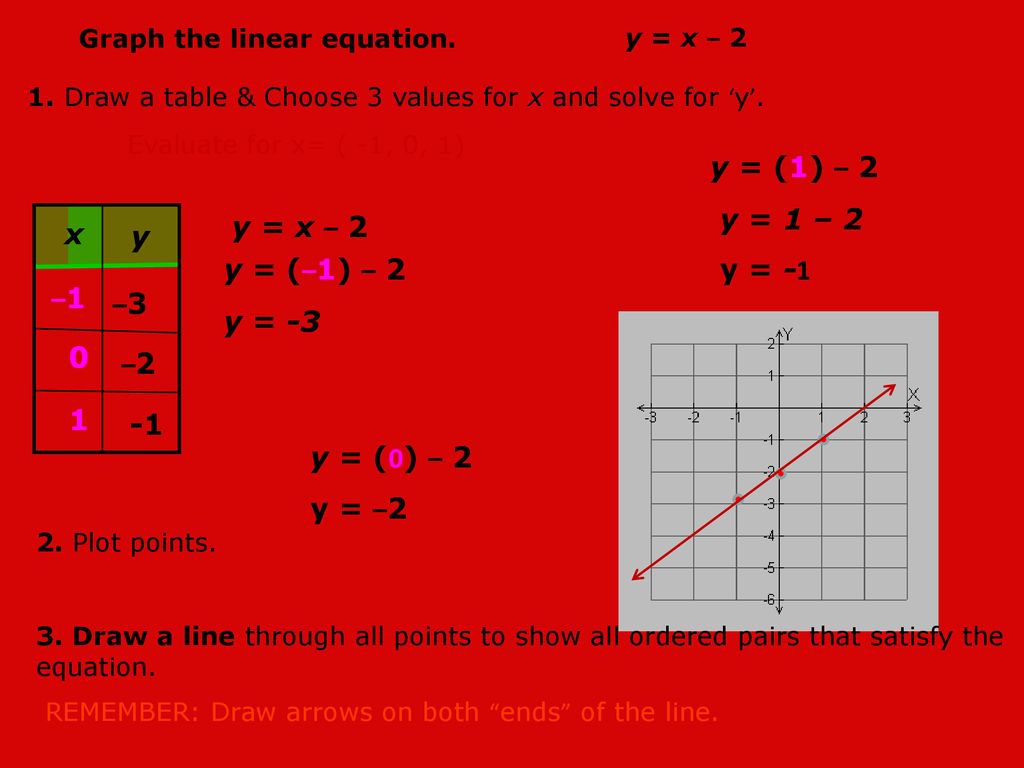
Y 1 2 Y 1 2 Y 1 Y X 2 X Y Y 1 2 Y 3 1 3 Ppt Download

Incoming Term: x^2+xy+y^2 グラフ,